Inhaltsverzeichnis
Decoding the wireless heating control Vaillant CalorMatic 340f (868MHz)
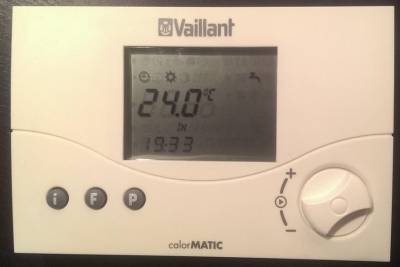
In our apartment, we have a wireless heating control system made by Vaillant (probably 8-10 years old). Since I recently started into Smart Home and Home Automation (well, so far, i have mainly set up a huge net of all different kinds of sensors and some light bulbs, as I have hardly anything that could be controlled wirelessly), of course I wanted to figure out how the wireless device works and in particular whether I could include it into my OpenHAB-based home network of things…
To detect and analyze the wireless signals, I'm using an RTL282x-based DVB-T dongle together with the RTL-SDR software.
Figuring out the Frequency
From the outside it does not give any indication about which frequency it uses.
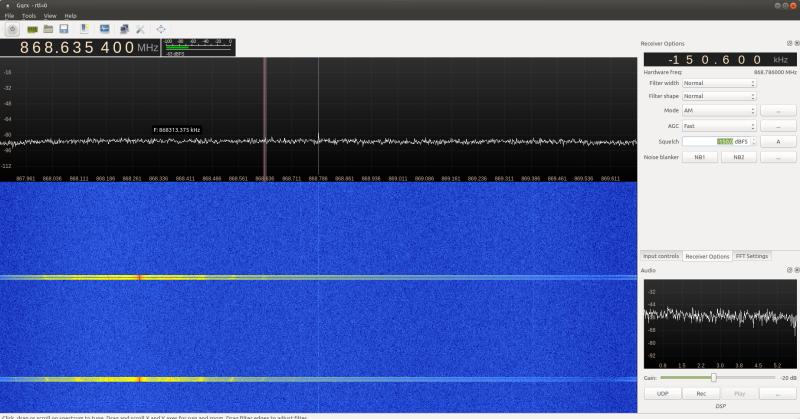
I figured it could only be one of the ISM bands, which in Europe are 433MHz, 868MHz and 2.4GHz and 5GHz. Since the latter two are mainly used for WLAN, Bluetooth, etc. that left me with two possible frequency ranges. Firing up gqrx, tuning to either 433MHz and 868MHz and changing the target temperature of the thermostat, gave me perfect bursts in the 868MHz band with peaks around 868.275 MHz:
The device
Curious as I am, I decided to disassemble the thermostat and check which chips and which transceiver are used:


While the back does not give any indication, dismantling the thermostat even further reveals the transceiver and its chip: an Infineon TDA5250D2 for the 868 MHz band.
Detecting the Signal
As we now know the frequency, let's take a look at the signal. There are multiple ways to transport digital data at a certain frequency. Most 433.92MHz devices use ASK (Amplitude Shift Keyring, the binary equivalent of amplitude modulation, i.e. AM) in its simplest form of OOK (On-Off-Keyring), which simply means that the frequency has either full amplitude (to indicate 1) or is absent (indicating 0). The 868MHz band and even more the 2.4GHz band use all different kinds of modulations, like FSK (frequency-shift keyring, i.e. the digital equivalent of FM) or even Phase-shift keyring, etc.
The transceiver data sheet states it is an ASK/FSK receiver for the 868MHz band, so let's first try to demodulate the signal as ASK. A hint that the signal really uses ASK can be seen from the waterfall chart in gqrx, as the peak stays at a fixed frequency, while a signal in FSK typically shows two peaks (as the modulation works by switching between two frequencies to indicate 0 and 1 respectively).
So, let's try demodulating the signal as ASK and in particular check for OOK.
In gqrx, I tune to the 868MHz band (near, but not exactly at the 868.275MHz we determined above) and record the signal to a wave file. To do this, make sure you set the mode to „AM“ (i.e. use ASK demodulation) and press the „Rec“ button at the bottom. This will create a file called gqrx_[ISO-Data]_[time]_[frequency].wav in your home directory, which holds the signal demodulated as a wave file. Even though the signal is not an actual sound, one can still use the audacity application to look at the waveform of the signal. Playing it as sound would not result in anything meaningfull except for a few clicks.
Recording a transmission by the thermostat and opening it in audacity gives this picture:
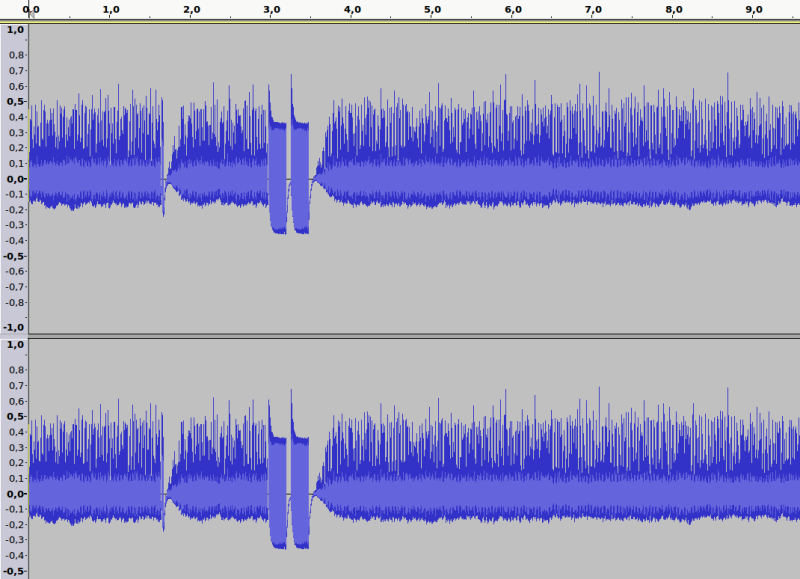
Not bad. We clearly see that there are two spots where the wave form obviously changes its form. Let's zoom in a little bit in audacity:
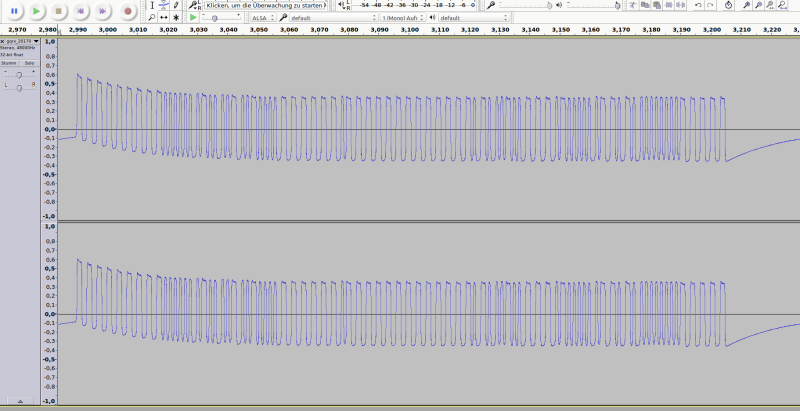
This signal seems to be repeated twice.
Yay, it seems our first guess to use ASK / OOK was right. We clearly see a signal with some long and short bursts, all with roughly the same amplitude and consistent on/off durations.
An alternative way to obtain a AM-demodulated signal for inspection in audacity is the command-line utility rtl_fm from the RTL-SDR project:
reinhold@zweistein:~$ rtl_fm -f 868275000 -M am -s 44100 `date -I`_test.sdr
Found 1 device(s):
0: Realtek, RTL2838UHIDIR, SN: 00000001
Using device 0: Generic RTL2832U OEM
Found Rafael Micro R820T tuner
Tuner gain set to automatic.
Tuned to 868528575 Hz.
Oversampling input by: 23x.
Oversampling output by: 1x.
Buffer size: 8.08ms
Exact sample rate is: 1014300.020041 Hz
Sampling at 1014300 S/s.
Output at 44100 Hz.
The resulting file (in the above example 2017-04-21_test.sdr) is not a wav file, but contains raw data that can be imported into audacity with the menu item File → Import → Raw data. The import settings are „Signed 16-bit PCM“, „Little Endian“, „1 channel (Mono)“ and the sampling rate is 44100. I had to zoom in vertically, as the signal appeared very faind. Personally, I find the resulting wave form easier to handle, as it shows the absolute values and shows the on/off signals even clearer:

What is clearly visible already in these images is that there are only two different lengths of the UP and the DOWN pulses: long and short. But what do they actually mean?
Figuring out the encoding of the signal
Now that we have a signal, let's try to understand the data that is sent over the ether. Unfortunately, the signal did not resemble anything that I had seen with my 433MHz devices. With them, either it was all short UP bursts of idential length and the 0/1 information as encoded in the DOWN time distance between the bursts (i.e. it was very short UP, and then either short or long DOWN), or the UP and DOWN signals together always had the same length (Pusle-width modulation, i.e. it was either short UP + long DOWN or long UP + short DOWN).
In our case, we have all different combinations of UP and DOWN: long UP + long DOWN, long UP + short DOWN, short UP + long DOWN, short UP + short DOWN. So maybe the up and down both encode one bit, i.e.
| UP | DOWN | binary value |
| short | short | 0 0 |
| short | long | 0 1 |
| long | short | 1 0 |
| long | long | 1 1 |
Let's put our hypthesis to the test: Simply transcribe our signal from above (and it's repeat sequence) using this decoding:
111111111111111110000000000001001000010000110000100000000111111111111100111111111111111111111111100110010000100111111110010000000000100001100110010000000000000000111111111 111111111111111110000000000001001000010000110000100000000111111111111100111111111100111111111111110011001000010011111111001000000000010011100110010000000000000000111111111
Hmm, we clearly see some longer sequences of 0 and 1 repeated (at the beginning and end it might make sense as kind of preamble and epilogue). However, the irritating fact is that the repeat is apparently not an exact repeat, especially towards the end all bits appear shifted. And in some other cases it does not even have the same signal length, but two bits more! Something can't be right….
Until I compared the signal and its „repeat“ in Audacity (signal is on top, repeat on the bottom):

Surprisingly, both signals always have exactly the same length in milliseconds and can be perfectly aligned, they just sometimes have a different number of UP/DOWNs!
Do you see where the difference starts and where it ends? Also, do you see why the bits in our simple transcription above are shifted?
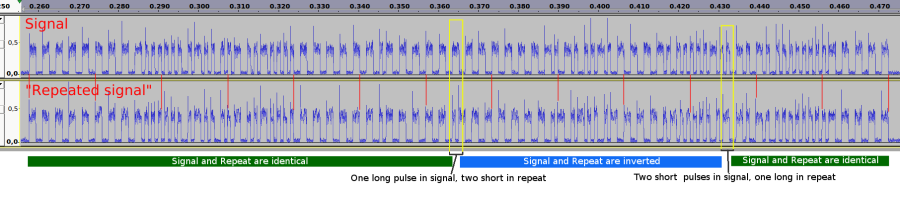
So clearly one long and two short pulses correspond… Something else to notice: There is a transition from UP to DOWN or from DOWN to UP every time interval that corresponds to one long pulse. Check my annotated signal: Every ten long pulses I placed a red bar. I.e. at regular intervals there is a guaranteed transition from UP to DOWN or vice versa. For short pulses there is an additional transition in between, but the regular transitions appear through the whole signal…
If we look at the signal in the application inspectrum (you need to use the output of a rtl_sdr recording!) and lay a grid with the proper width over the whole signal, we can confirm that no long UP or long DOWN pulses cross a grid line:
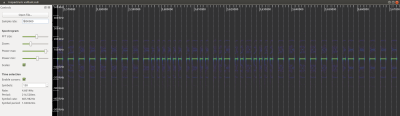
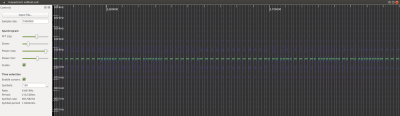
For now, we have determined that the basic time interval of the signal is that of one short pulse and the long pulses are exactly twice as long. Inspectrum also tells us that one signal (without repeat) is 215ms long with 130 symbols and the symbol rate (data frequency) is 606 Hz, i.e. there are 606 long intervals per second.
So, every 1.65ms there is a transition (i.e. we have a binary base signal of 606 Hz), and sometimes there is an additional transition halfway in between.
So let's transcribe each long UP signal as 11, each long DOWN signal as 00 and each time period with a transition from DOWN to UP as 01 and from UP to DOWN as 10. I.e. we transcribe our binary signal as OOK with a base frequency of 1212 Hz. The signal and the repeat in our example above would then be:
11001100110011001100110011001100110101010101010010110101001010110010101101010101001100110011001100110011001011001100110011001100110011001100110011001100110011010011010010101101001100110011001101001010101010110101001101001101001010101010101010110011001100110011 00000000000000000000000000000000000 11001100110011001100110011001100110101010101010010110101001010110010101101010101001100110011001100110011001011001100110011001100101100110011001100110011001100101100101101010010110011001100110010110101010101001011001101001101001010101010101010110011001100110011
Getting a file of 0/1 states
Recording to a .wav file and then looking at it in audacity to see the binary signal helps a lot when trying to understand the structure of a signal, but it is not feasible for testing multiple combinations. It would simply take way to long to transcribe signals to 0/1. So let's use a program to do this: gnuradio, in particular the gnuradio companion (GRC).
GNUradio is a signal processing framework built on top of Python, with the GNUradio Companion (GRC) being a really nice graphical frontend to build signal processing pipelines. I use the following flow to read raw data from my RTL2838 DVB-T stick, convert it to a 0/1 time series (where each short time interval is converted to either 0 or 1):
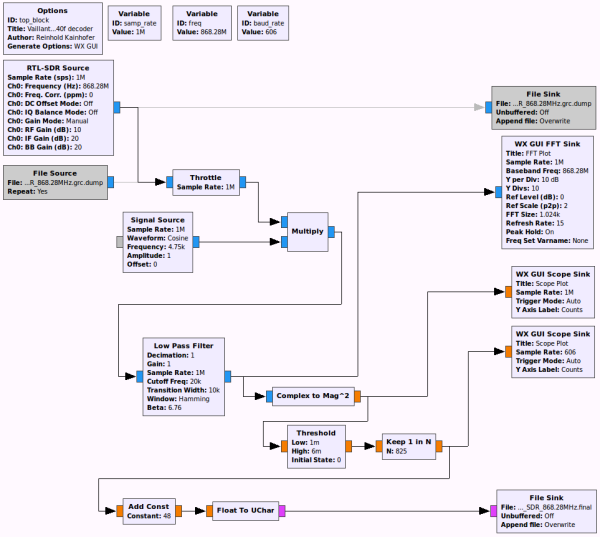
The corresponding .grc file can be downloaded here. What this GRC file does:
- RTL-SDR Source: Read data from the RTL-SDR source (the DVB-T stick) with a sample rate of 1 million samples/sec, tuned to 868.28MHz
- Multiply: Shift the peak of the signal to the center so we have best signal (the shift depends on the individual stick, so you might need to modify this) (the Multiply)
- Low Pass Filter: Cut off everything outside a frequency range around the desired frequency
- Complex to Mag^2: the ASK / OOK demodulation (i.e. extract the amplitude of the signal, holding the 0/1 information)
- Threshold: convert the amplitude to pure 0/1 values (depending on your signal strength and the noise, you might need to adjust the parameters)
- Keep 1 in N: As we read 1m samples per second from the DVB-T stick, each short burst in our signal contains 825 data points (the 606 Hz symbol rate, where each „symbol“ contains two half-intervals, i.e. each second contains 606*2 short intervals ⇒ 1.000.000/(606*2)=825)
- Add Const + Float To UChar: Convert the numbers 0 and 1 to the ASCII characters '0' and '1'
The result is a file containing the characters 0 and 1 for our signal, where each digit represents the on/off state of each short pulse of length 0.825 ms.
Extracting the binary information
Now we have the raw file containing the signal, let's find out the binary interpretation of the signal.
Manchester Encoding?
Above we noticed that the signal had periodic transitions from high to low and vice versa every. For signal processing hardware, this makes it easy to synchronize clocks at the receiver side. One of the most famous such encodings is Manchester encoding, where there is one transition in the center of each bit period (and potentially also between bit periods, but they are irrelevant). In particular, a 0→1 transition means a digital 0 and a 1→0 transition means a digital 1 (in IEEE 802.3). Let's check if our signal is Manchester encoded.
Remember, the original signal was:
11001100110011001100110011001100110101010101010010110101001010110....
For Manchester decoding, let's split it up into bit periods that always contain a transition in their middle (add the 0 at the beginning, which we didn't transcribe above):
01|10|01|10|01|10|01|10|01|10|01|10|01|10|01|10|01|10|10|10|10|10|10|10|01|01|10|10|10|01|01|01|10|....
We only have 01 (meaning 1) and 10 (meaning 0), so let's transcribe the signal with these replacements:
101010101010101010000000....
Transcribing the signal manually was way too cumbersome, so I wrote a little C program to do the Manchester decoding by piping the output of gnuradio-companion through it (or alternatively, any text file containing thesignal): Manchester_decode.c
Transcribing the whole signal and its repeat, we end up with:
01010101010101010111111100111000100011111010101010101001010101010101010101010101101100011010101011000000111011011000000000101010101 01010101010101010111111100111000100011111010101010101001010101010010101010101010010011100101010100111111001011011000000000101010101
Hmm, a lot of alternating 1 and 0 sequences. And the „repeat“ is quite different from the signal (albeit it is mainly just inverted). But for some signals I observed (in particular with low battery status), the inversion lasted almost until the end:
01010101010101010111111100111000100011111010101010101001010101010101010101011010010011100010101011000000110101011000000000101010101 01010101010101010111111100111000100011111010101010101001010101010010101010100101101100011101010100111111000000111011111111101010101
This doesn't look too convincing. So, probably not Manchester code.
XOR'ing with a 1100 base wave
If we look at the signal again (11001100110011001100…), it starts with a perfect square wave that is responsible for the period transitions. After the initial preamble, the signal deviates, but the key feature of the underlying square wave is always present. What if the information is actually contained in the difference to the square wave 1100110011001100…? If we XOR the signal with a perfect square wave 110011001100110011001100… we simply remove those periodic transitions that are only meant to help the receiver sync its clock. Does that lead to more useful data?
0000000000000000000000000000000000011001100110000111100111100111111001111001100111111111111111111111111111100000000000000000000000000000000000000000000000000001111110000110000111111111111111111000011001100111100111111000000111100110011001100111111111111111111111 0000000000000000000000000000000000011001100110000111100111100111111001111001100111111111111111111111111111100000000000000000000001111111111111111111111111111110000001111001111000000000000000000111100110011000011111111000000111100110011001100111111111111111111111
Actually, the signal looks easier to understand visually, but the huge differences between the signal and its „repeat“ are still there. Even worse: The 11001100110011 epilogue at the end of the signal is apparently NOT synchronized with a square wave starting with the square wave preamble, so we end up with 11111 at the end.
Again, this is probably also not the way to go.
Transition or not?
Since our signal appears to guarantee a transition every two digits, there cannot be any information encoded in those transitions. However, between those periodic transitions, sometimes there is another transition and for other periods there is no further transition. What if the information is actually encoded in whether there is a transition or not?
Let's split our signal at the periodic transitions (Manchester encoding split it halfway in between, now we are splitting it differently!):
11|00|11|00|11|00|11|00|11|00|11|00|11|00|11|00|11|01|01|01|01|01|01|00|10|11|01|01|00|10|10|11|0.... 0 0
We now have four different parts, 00, 01, 10 and 11. 00 and 11 don't have a transition, so let's say this encodes 0 and 01 and 10 have a transition, which we understand as a binary 1. This leads to the transcription
11|00|11|00|11|00|11|00|11|00|11|00|11|00|11|00|11|01|01|01|01|01|01|00|10|11|01|01|00|10|10|11|0.... 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0
Again, I wrote a little C program to automate this decoding: Vaillant_decode.c
Our signal and the „repeat“ from above now become:
00000000000000000111111010110110011011110000000000000100000000000000000000000001001011010000000010111110110010010111111110000000000 00000000000000000111111010110110011011110000000000000100000000001000000000000001001011010000000010111110100010010111111110000000000
Not bad. In particular, the signal and its repeat only differ at two places (the two spots that we already identified in audacity)…
It looks like we have extracted the actual binary information from the 868MHz signal.
UPDATE: After some more reading, it seems that this type of encoding is also known as Differential Manchester encoding or Bi-Phase Mark Code.
Decoding the Messages
Now that we know the binary contents of the messages sent by the thermostat to the boiler, the next step is to understand what these messages actually mean. I'll describe this decoding in a separate post.
UPDATE: Bit stuffing -- but WHY?
During my tests of the wireless control, I collected various different signals. Trying to group them into octets for bytes, I ended up with a dilemma: I realized that the second-to-last byte should be 0xFF and the one before was probably some kid of checksum. That left me with 9 bits before that checksum byte:
<html> <pre>00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00010001 00101101 00000000 <span style=„color: red; font-weight: bold“>101111101</span> 10000010 11111111 000000000 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00010001 00101101 00000000 <span style=„color: red; font-weight: bold“>101111101</span> 00000010 11111111 000000000 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00010001 00000000 00000000 <span style=„color: red; font-weight: bold“>101111101</span> 10101111 11111111 000000000 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00010001 00000000 00000000 <span style=„color: red; font-weight: bold“>101111101</span> 00101111 11111111 000000000 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00000001 00000000 00000000 <span style=„color: red; font-weight: bold“>101111101</span> 10111110 11111111 <span style=„color: red; font-weight: bold“>1</span>000000000 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00000001 01111100 00000000 <span style=„color: red; font-weight: bold“>010111110</span> 11111011 01111111 <span style=„color: red; font-weight: bold“>11</span>0000000 00 00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00000001 01111100 00000000 <span style=„color: red; font-weight: bold“>010111110</span> 10111110 01111111 <span style=„color: red; font-weight: bold“>11</span>0000000 00 </pre></html>
The first four observations were among the most frequent signals.
In this table, I already split the binary signal into octets, i.e. bytes. Since the full signal has 129-131 bits, some extra bits need to be included to form 9-bit parts somewhere.
As my reasoning in part 2 shows, that extra byte must be before the final three bytes, but after the fifth-to-last one. So we have the 9-bit sequence 101111101 that we must make sense of. Even worse, the last two observations appear to be shifted by one additional bit after a bit sequence of 01111100.
After some googling, I stumbled upon the framing approach in the High-Level Data Link Control, where the frames start with 0x7e=01111110 and the bit stuffing in the data part means that after five consecutive 1 bits, an extra 0 bit is included, which must be removed at the receiving end. Indeed, the 101111101 bit sequence is the only appearance of five consecutive 1 bits in the first few examples. Some other signals also contained sequences of 5 (but not more) consecutive 1 bits, followed by a seemingly spurious zero… Bit stuffing would explain this spurious 0 bit and even demand to remove it before interpreting the signal. If we do bit unstuffing on our signals (again, using a little helper utility Vaillant_decode_bitstuff.c), suddenly the signal aligns perfectly into octets to form bytes:
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00010001 00101101 00000000 10111111 10000010 11111111 00000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00010001 00101101 00000000 10111111 00000010 11111111 00000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00010001 00000000 00000000 10111111 10101111 11111111 00000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00010001 00000000 00000000 10111111 00101111 11111111 00000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00000001 00000000 00000000 10111111 10111111 11111111 00000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 00000000 00000001 01111100 00000000 10111111 11111101 11111111 0000000 |
00000000 00000000 01111110 10110110 01101111 00000000 00000100 00000000 10000000 00000001 01111100 00000000 10111111 01111101 11111111 0000000 |
So, the pysical layer appears to be encoded using differential Manchester coding, after bit-stuffing. Somehow to me this does not make too much sense, as bit-stuffing is used mainly to cause state transitions at last every five bits to allow the receiver to synchronize its clock. However, the underlying differential Manchester coding of our signal already ensures a transition after every bit, so there is no need in my eyes for additional bit-stuffing.
But as the evidence is so overwhelmingly in favor of bit-stuffing, let's accept that the signal is bit-stuffed (except for the two final 0xFF 00 bytes) and then transmitted using differential Manchester coding.
Finally: Decoding the Messages
Now that we finally know the binary contents of the messages sent by the thermostat to the boiler, the next step is to understand what these messages actually mean. I'll describe this decoding in a separate post.